2024年度のノーベル物理学賞、ノーベル化学賞がともにAI関連の受賞であったことは驚きをもって伝えられた。なぜAI関連の受賞が相次いだのか? 人工ニューラルネットワークの概念を確立し、深層学習(ディープラーニング)の発展に大きく貢献したプリンストン大学名誉教授のジョン・ホップフィールドとトロント大学名誉教授のジェフリー・ヒントンのノーベル物理学賞受賞の画期性とは。その背景には、まず2021年度の「複雑物理系」のノーベル物理学賞受賞があり、今回の受賞はそれと関連して分野を越境してもたらされたものであると日本における複雑系・カオス理論研究の第一人者の津田一郎氏は分析。3回にわたって解説記事をお届けする。(全3回の#1)
◆◆◆
「最近のノーベル物理学賞は攻めている」。複雑物理系に次いで2024年度は人工知能に
2024年度のノーベル物理学賞は近年の人工知能(AI)の爆発的な発展の基礎を作った人工神経回路網(ANN)の研究が対象になった。巷では、「最近ノーベル物理学賞は攻めている」という感想が聞かれる。
2021年度は「複雑物理系」に与えられたことは記憶に新しい。スピングラス理論、気象から気候変動への時間空間スケールを超えた複雑な秩序形成を基盤にした研究に物理学賞が贈られた。この年も従来の素粒子・宇宙分野、物性分野をほぼ交互にという“鉄則”を破った受賞だった。
ただし、我が国における報道は「日本人がノーベル賞をとった」、「気候変動がノーベル賞をとった」の一点張りで、ノーベル賞委員会(以下、委員会)の発表を完全に無視したものであった。委員会は記者発表用、一般向け、専門家向けの3種類のレポートをノーベル賞発表と同時にネット配信している。当日のオンライン配信の記者発表と共にそれらのレポートを読むと、2021年度の受賞対象が複雑物理系(Complex Physical Systems)であることが一目瞭然であった。カオス研究や複雑系研究での盟友である金子邦彦とメールで喜びの感想を交換したりもした。

筆者は当時同僚になっていた元大手新聞社科学担当記者に不満を言った。意見が一致したこの元同僚の計らいで、同様の感想を持っていた日経新聞と毎日新聞の記者を紹介いただき、インタビューを受けた。その内容が、「誤解された眞鍋氏のノーベル賞 複雑系の科学で評価」と題する記事として日経新聞電子版(2021年12月1日午後2時)に掲載された。さらに、毎日新聞は翌年のノーベル賞発表前に特集を組み(2022年9月28日午前7時毎日新聞オンラインと9月29日毎日新聞朝刊)、物理学賞に関する記事の中で前年度の眞鍋らの受賞に触れ、複雑系が注目され今後の受賞に影響を与える可能性について論じた。
複雑系、そのブームと日本における末路
複雑系が世界的に注目を集めるようになったのは1980年代半ばから1990年代にかけてだった。日本でも一時ブームになり、金子邦彦、津田一郎、池上高志、伊庭幸人など当時の物性基礎論・統計力学の若手が中心になって京都大学基礎物理学研究所の長期研究集会として6年間研究会を開催したのが一つの契機となって研究が発展していった。ヨーロッパやアメリカでは複雑系に関する研究所が次々とできていき、現在に至るまで活動を続けている。
他方、我が国においてはブームに乗って複雑系を冠した学科や講座、さらにはバーチャルな研究施設ができたが、複雑系を研究していた若手は呼ばれなかった。そして、ブームが去るとあっという間に学科名、講座名は替わっていった。その前の時代から続くカオス研究を含め複雑系研究は物理分野においてはいかもののように言われ、研究を続けていると、まだそんなものやってるんですか、などと言われたのである(ただし、数学・数理科学分野は違っていてカオスはむろんのこと複雑系に関しても新しい研究動向として捉え、その数学・数理科学研究を学会としても推進した。人工知能分野では中島秀之や竹内郁雄らいち早く複雑系に着目した研究者がいたことで複雑系の概念は守られた。中島が学長だった未来大では複雑系科学科を複雑系知能学科という名前に変更して現在に至っている。しかしこれらは稀有なことであった)。
分野を越境するノーベル物理学賞――AI受賞は2021年度の複雑物理系受賞と大いに関係している
それがどうであろうか。カオスは2021年度のノーベル物理学賞の対象になった研究の基盤を作り、受賞対象は複雑物理系であったのである。複雑系は様々な分野に共通して存在するので、あえて記すなら複雑化学系、複雑生命系、複雑脳神経系、複雑知能系、複雑工学系、複雑経済系、複雑社会科学系、複雑デザイン系、複雑医療系、複雑数理系などなど明確にイメージできる個別複雑系分野は実に多いのである。そして、今回の人工知能分野での受賞は表だっては表明されていないがまた複雑系と大いに関係しているのである。今後、受賞対象はこのような各分野へと越境していくことだろう。それを目撃できるとしたら幸福なことである。
スピングラスとは何か? 2021年度のノーベル物理学賞を振り返る
今年度の受賞と関係があるので、まず2021年度の受賞対象の研究を簡単に振り返っておく。ジョルジュ・パリジに対してはスピングラスの統計物理学による機構解明を行ったことが評価の対象だった。後述するように、スピングラスは今年度の受賞とも関係している。
スピングラスというのは、磁性を示さない物質(例えば銅)の中に少量の強磁性体(例えば鉄)を混入させた合金のことで、独特の磁性を示す。スピンとは自転する電子の角運動量のことで、物質中で上向きスピンと下向きスピンは互いに打ち消しあうが、打ち消しあわないスピンが残ればその物質は磁性を持つ。鉄は強磁性体で、すべてのスピンの向きがそろう傾向にあり強い磁性を示す。
スピングラスでは磁性を示さない物質に磁性を示す物質が少量混入しているので、各原子でのスピンの向きが必ずしもそろわなくなる。図1は三角形の各頂点に原子が配置されたときのフラストレートしたスピン状態を表している。すべてのスピンが上向きか下向きでそろっていればエネルギー的には低い安定な状態が作られるが、図1のように一つのスピンが反対を向くだけで、最安定な状態ではなくなる。
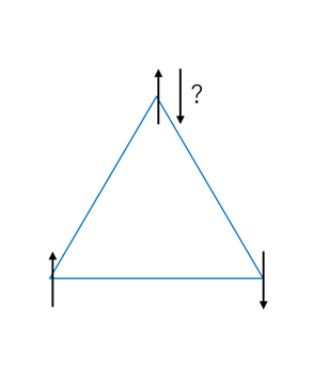
三角格子状に配置されたスピンは一つが反対向きになると、多重安定な状態が発生する。図はTHE NOBEL PRIZE IN PHYSICS 2021 POPULAR SCIENCE BACKGROUNDを参考に筆者が描いた。
図の三角形の一番上の頂点のスピンは上を向いても下を向いても系全体としては同じエネルギー状態なので、どちらを向くかが決められない。スピングラスではこういったフラストレートしたスピン状態が起こるために、各原子のスピンの向きがバラバラな状態で凍結される(図2)。

緑は銅、赤は鉄、矢印は鉄原子のスピン状態を表す。図はTHE NOBEL PRIZE IN PHYSICS 2021 POPULAR SCIENCE BACKGROUNDを参考に筆者が描いた。
スピングラスも複雑物理系である、と捉えたノーベル賞委員会
スピングラスは複雑物理系であると委員会は捉えた。パリジは近年鳥の群れの研究など他の複雑系の研究にも精力的に取り組んでいた。委員会は気象現象や気候変動も典型的な複雑物理系だと捉えた。数日から1週間程度の気象変化がカオスであり予測が不可能である複雑現象だという認識は、“バタフライ・エフェクト[i]”で知られるエドワード・ローレンツ(1991年度京都賞)によって最初に与えられた。ローレンツカオスの発見である。この発見が一つの契機となりカオス力学系(非線形力学系)という分野が数学、物理学の中で確立していき、工学の各分野にも大きな影響を与えた。残念ながら、ローレンツは亡くなってしまったので彼自身は今回の受賞者にはなれなかったが、クラウド・ハッセルマンらがローレンツカオスを気候変動の理論の基礎に置いた。

「奇跡の年」(Annus mirabilis)と呼ばれる1905年のアルベルト・アインシュタインの二つ目の論文はブラウン運動の理論であり、ミクロな分子の熱的なランダム運動によってマクロなブラウン粒子に拡散運動が起こることを示したものだ。気候変動現象ではスケールを変えてこれと同じことが起こっているのではないかとハッセルマンらは考えた。マクロな気象現象がローレンツの指摘のようにカオスならば、さらにスケールの大きな10年程度の地球規模の現象である気候変動は拡散的な方程式に従い、その導出は統計力学ではおなじみのランジュバン方程式[ii]から導出されるフォッカー・プランク方程式[iii]に基づくものになるだろうと予想した。
気候変動問題もまた複雑物理系である理由
他方、気候変動問題を一次元鉛直方向の数理モデルとして定式化し、大規模な計算機実験を行ったのが眞鍋叔郎である。眞鍋は地球大気の二酸化炭素濃度が2倍になれば、大気温度が約2.3℃上昇することを計算で導き出した。この問題は、1896年にスヴァンテ・アレーニウス(1903年ノーベル化学賞受賞、アインシュタインが1921年度ノーベル物理学賞を「光電効果の理論」によって受賞した時のノーベル賞委員会委員長(後述))が「二酸化炭素が2倍になると大気温度が6℃上昇する」と予測して以来の問題であるので、当然委員会は眞鍋の結果に注目していた。おりしも、気候変動問題、地球温暖化問題が深刻さを増しており世界中の関心の的となっていたことも受賞を後押ししたと思われる。この気象カオスから導かれる気候変動問題も複雑物理系であると委員会は認識したのだった。
[i] バタフライ・エフェクト 力学系の状態にわずかな変化を与えると、そのわずかな変化が無かった場合とはその後の系(システム)の状態が大きく異なってしまうという現象。気象学者ローレンツによる「蝶がはばたく程度の非常に小さな撹乱でも遠くの場所の気象に影響を与えるか」という問いに由来する。
[ii] ランジュバン方程式 確率変数の時間変化が確率変数の減衰項と外部からの揺動力で与えられるような関係を表す常微分方程式をフランスの物理学者ランジュバンにちなんでランジュバン方程式という。
[iii] フォッカー・プランク方程式 確率変数の分布関数が従う偏微分方程式で、分布関数の時間に関する一階微分と確率変数に関する二階微分で近似した分布関数の拡散方程式をフォッカー・プランク方程式という。ランジュバン方程式が与えられると対応するフォッカー・プランク方程式を決めることができる。
















